华夏银行首席信息官、龙盈智达(北京)科技有限公司董事长 吴永飞

  《“十四五”数字经济发展规划》指出，要加快推动数字产业化，增强关键技术创新能力，瞄准传感器、量子信息、网络通信、集成电路、关键软件、大数据、人工智能、区块链、新材料等战略性前瞻性领域。二十大报告指出“一些关键核心技术实现突破，战略性新兴产业发展壮大，载人航天、探月探火、深海深地探测、超级计算机、卫星导航、量子信息、核电技术、大飞机制造、生物医药等取得重大成果，进入创新型国家行列”。目前，已有机构开始将量子算法运用在投资组合、资产定价等金融领域的实证研究中。中国私募基金风险管理研究中心发布的《中国量化基金白皮书》数据显示，当前，中国量化基金管理规模已超1万亿元。量子计算具备的潜在算力优势和量子通信形成的安全传输能力与量化投资领域的大规模数据运算及安全交易天然匹配，量子科技与量化金融的结合有望给金融领域带来飞跃性的技术变革。

  本文聚焦量子算法在我国二级市场行业轮动策略的实证研究，将量子近似优化算法(Quantum Approximate Optimization Algorithm，QAOA)应用于资产组合构建过程中的行业权重配置环节，以期为量子科技助力量化金融策略优化提供新思路。

  一、量子近似优化算法赋能金融投资组合构建

  量子近似优化算法由Edward Farhi等人在2014年提出。该算法是一种经典计算与量子计算的混合算法，可用于解决组合优化问题、最大分割问题等难题，尤其在解决某些NP-hard问题时有明显的加速效果，可以在多项式复杂度下给出问题的近似解，适用于投资组合、风险管理和干线物流等场景。

  针对量子优化算法在投资组合领域的应用，学界已开展了一系列研究探索。Iordanis Kerenidis等(2019)开发了第一个用于约束投资组合优化问题的量子算法。G.G.Guerreschi和A.Y.Matsuura(2019)指出QAOA在解决最大分割问题时需要数百个量子比特加速。Stuart Hadfiel等(2019)介绍了量子交替算法，该算法是量子近似算法的拓展，支持更大范围、更有效的状态集，可以解决各种近似优化、精确优化和采样问题。White Nathan等(2021)使用QAOA满足中等噪声规模量子(Noisy Intermediate-Scale Quantum，NISQ)计算机的约束条件，研究投资组合优化问题，以最大限度地减少投资组合波动，同时最大化预期回报。Samuel Fern á ndez-Lorenzo等(2021)运用启发式量子算法QAOA研究投资约束下的证券组合，并通过数值模拟比较相关量子分析和经典优化器的性能。N.N.Hegade等(2021)认为数字化反绝热量子计算是接近NISQ时代工业应用量子优势的高级范式，并应用这一概念来研究离散平均方差投资组合优化问题，讨论了该方法在QAOA和DC-QAOA等变分量子算法上的增强性能。

  当前，投资组合领域仍存在诸多关键问题等待量子算法的赋能，其中关于行业轮动的研究是典型场景之一。行业轮动是量化投资中常用的一种策略，利用不同投资品种上涨趋势的强弱对行业品种进行切换，以达到投资收益最大化的目的。该策略通常会受到行业景气度、行业周期、市场资金等因素的影响。作为行业轮动策略的理论基础之一，2004年美林证券基于美国1973—2004年的历史交易数据，提出了著名的“美林投资时钟”理论，该理论作为资产配置领域的经典理论，将资产轮动、行业策略、经济周期联系起来。本文运用量子近似优化算法开展我国二级市场行业轮动问题的研究，旨在通过量子算法生成标的行业的配置权重，从而实现在波动较低情况下的组合最优收益。

  二、量子近似优化算法在行业轮动策略中的实证研究

  1.业务理解

  一般而言，投资组合的构建包括标的筛选和权重配置两大模块，在本文针对行业轮动策略的研究中，标的筛选部分基于价格噪音方法论，权重配置部分主要运用量子近似优化算法实现。

  价格噪音方法论是指运用分形效率这一关键指标实现行业标的筛选。有研究表明，测量价格噪音是识别行情变化模式的可行方法之一，通过价格噪音可识别出数据中的趋势。而分形效率是一种测量价格噪声的重要指标，当该指标数值接近1时，表示市场此时呈现出强大的趋势。

  同时，为探寻下一个周期最优的资产权重，本文使用QAOA进行权重配置时的创新如下：首先将原有标的资产的收益率序列均值方差变为权重组合后的收益率序列均值方差指标，然后使用迭代思路解决量子比特数受限的问题，不断使用QAOA进行当前组合下最优权重组合的计算并持续迭代，直至得到最优解。

  为进一步解释算法思想，本文以3个目标资产为例，尝试使用QAOA进行资产权重分配(如图1所示)。

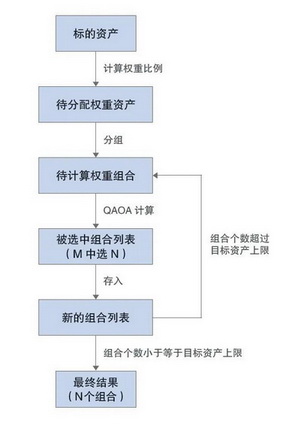
图1 使用量子近似优化算法解决权重分配问题的流程

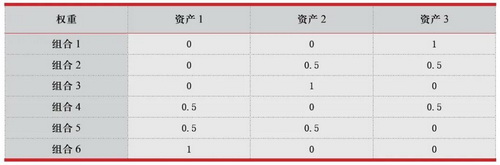
  假设对3个目标资产进行总权重为100%的权重分配，权重的分配间隔为50%，即可选权重为0%、50%和100%，所有可能的组合情况见表1。组合1代表资产1和资产2均不选择，资产3的权重为1即100%。当资产组合较少时无需迭代，直接将6个组合的均值与方差作为QAOA组合的输入进行组合选择，此时的结果即为最优的资产权重。

表1 3个目标资产权重间隔为0.5时的所有权重组合

  当资产过多而无法满足量子比特数限制时，如10个资产进行100%的权重分配，权重的间隔为25%，所有可能的资产组合共715个，则需要迭代得到最优组合权重。为保证每次QAOA的执行效率，研究团队设置量子比特为8个、目标资产为3个，即每次QAOA可以从8个组合中择优选出3个。第一次迭代时，从组合1到组合8可得到3个最优组合，从组合9到组合18可得到3个最优组合，以此类推，715个组合共需要进行90次计算(组合数/一次处理组合数即715/8=89.375)，第一次迭代会存储270个权重组合(计算次数×最优组合数即90×3=270)，重复计算和存储过程不断进行第二次、第三次迭代，直到得到最优的3个组合为止。

  2.数据理解和数据准备

  实证研究中，针对行业权重分配问题，本文选择中信证券指数体系中行业及大类板块系列指数的一级行业共29个指数作为初始资产池，采集2017年1月3日—2022年6月30日的共1333个交易日的数据。

  首先使用价格噪音概念中的分形效率对29个指数数据进行筛选识别，一般每3个月进行一次标的资产筛选更新，即从29个行业中选出10个分形效率趋近于0(即有较大的概率出现行业轮动)的行业作为标的资产，从而解答“选择哪些行业投资”的问题。在得到最近一次更新的行业列表后，使用本文创新提出的量子近似优化权重配置方法来进行10个目标行业的权重分配，即回答行业轮动策略中“每个行业投资多少”的问题。

  3.模型应用

  针对QAOA进行组合权重配置部分，组合的风险可以用期望收益率的波动率来衡量，其中期望收益率可通过组合收益率进行计算，波动率通过收益率协方差矩阵进行计算。模型的目标函数为：

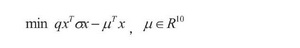
  定义资产的预期回报即收益率的均值为μ：

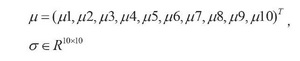
  其中，σ为不同资产之间收益率的协方差矩阵;q表示投资者的风险偏好，假设投资者为风险中性(q=0.5)。为解决权重分配问题，如前文所述，利用迭代思想，通过量子算法不断给出量子比特为8、目标资产为3的最优组合。

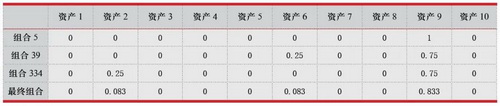
  以一次计算为例，迭代结束后得到的组合及各自权重见表2，即在715个组合中最终选出的3个组合为组合5、组合39、组合334，平均3个组合后的最终权重为资产2分配8.33%、资产6分配8.33%、资产9分配83.33%。通过将每次组合权重作为下一轮再平衡的策略，就可以使原本擅长解决组合标的筛选问题的QAOA转化为解决资产权重分配问题，从而得到整个回测区间不同时间段内最优的行业及各自权重。

表2 3个目标资产权重间隔为0.25时的最终权重组合

  4.模型评估

  基于前文所述的方法论，通过数据实验，每3个月进行一次标的资产更新，每3天进行一次再平衡，研究团队创新运用QAOA对行业轮动的标的资产进行权重分配，并最终得到的净值曲线(如图2所示)，策略净值评价指标见表3。本文使用中信证券一级行业中的综合行业作为基准策略，将QAOA给出最终权重的策略超额收益的净值与单纯通过价格噪音方法选出的策略超额收益的净值进行对比，可以发现从年化收益率(RET)、波动率(STD)、最大回撤率(MDD)、夏普比率(SHARPE)、索提诺比率(SORTINO)等指标来看，基于QAOA的行业轮动策略均优于纯量化的价格噪音策略。

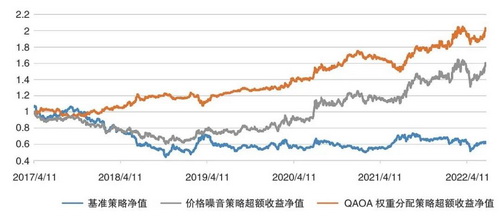
图2 基准策略净值、价格噪音策略超额收益净值、QAOA策略超额收益净值曲线

表3 策略净值评价指标

  三、结语

  针对金融市场中二级市场行业轮动问题，本文创新运用量子近似优化算法，通过将单一资产均值与方差的设定调整为权重组合后的指标，并运用迭代思想，实现了满足当前量子比特数要求的量子近似优化算法在组合权重配置领域的应用。本研究将量子近似优化算法从其擅长的组合标的筛选领域引入权重配置领域，为解决二级市场投资组合优化问题提供了新思路。长远来看，量子近似优化算法不仅可以适用于二级市场，还可以应用于商业银行智能资管、客户精准营销等多个领域，具有向银行、证券、基金、期货以及其他行业推广的广阔前景。

作者：

  华夏银行首席信息官、龙盈智达(北京)科技有限公司董事长 吴永飞

  华夏银行信息科技部副总经理、龙盈智达(北京)科技有限公司首席数据科学家 王彦博

  华夏银行信息科技部 刘小伟

  龙盈智达(北京)科技有限公司 杨璇 王一多

  感谢国开启科量子技术(安徽)有限公司对本文的支持。龙盈智达(北京)科技有限公司王子珺、白晶、李翠婷对本文亦有贡献。

  本文受北京市科技计划《量子金融云平台关键技术研发及示范应用》项目支持，项目编号为Z231100001323001。